Training Neural Networks with Differential Evolution for Reinforcement Learning Tasks
Differential Evolution is an evolutionary method that evolves a population to optimize the given loss function. In each generation of differential evolution, a candidate population is created and parents are replaced with better performing children. To create this candidate population, parents are crossovered with mutation vectors that are
calculated with random individuals from the population. There are different strategies in differential evolution which affects how the mutation vector is calculated. For example, in best1_bin strategy, the mutation vector is calculated as $$\text{best_individual} + \text{differential_weight} * (\text{random_individual}_1 - \text{random_individual}_2)$$ Differential weight is also called mutation factor in the literature. For all experiments, best1_bin strategy is used.
For the recombination(crossover) part, each weight in parent is replaced with a mutated weight with a probability. This probability is called crossover probability in the literature.
Python pseudocode for creating a candidate population with best1_bin strategy;
for p in population:
p1, p2 = random.choice(population, 2)
diff = p1.weights - p2.weights
mutation_vector = population[best_id].weights + mutation_factor * diff
mask = np.random.rand(len(mutation_vector)) <= crossover_probability
p.weights[mask] = mutation_vector[mask]
You can read more about it from https://en.wikipedia.org/wiki/Differential_evolution .
When I learn a new optimization algorithm, I always try it with reinforcement learning tasks to see how well it performs in this area of AI. Recently, I implemented a library for Natural Evolution Strategies and since evolutionary algorithms are very similar in terms of implementation, it was really easy to modify the nes-torch to implement a differential evolution library.
In all experiments the LunarLander-v2 environment from OpenAI gym library is used. My first experiment was training a feedforward network that has no hidden layers. Also, in every experiment I used population size of 256 and varied only the mutation factor and the crossover probability hyperparameters which are 0.5 and 0.7 respectively for this experiment.
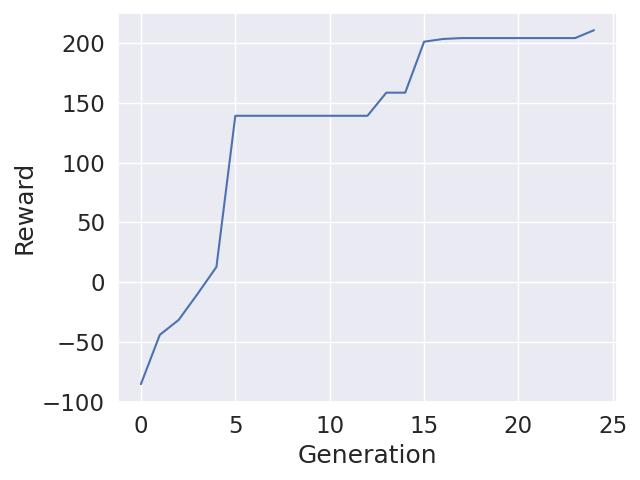
LunarLander-v2, No Hidden Layer, Mutation Factor: 0.5, Crossover Probability: 0.7
Above graph shows that differential evolution can quickly get good rewards in reinforcement learning tasks even with a really small network. Unfortunately, with the same settings, when the network size is increased, the results are not as good as expected.
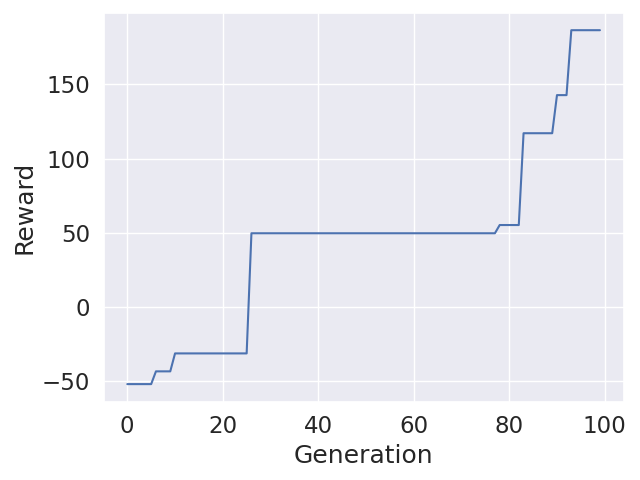
1 Hidden Layer with Size of 16, Mutation Factor: 0.5, Crossover Probability: 0.7
I found out that lower crossover probabilities work much better with high dimensionality. I tried really low values such as 0.05 and it trained very well.
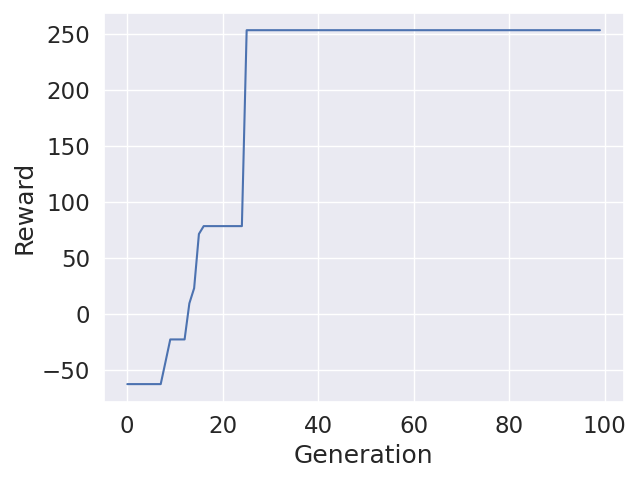
1 Hidden Layer with Size of 16, Mutation Factor: 0.5, Crossover Probability: 0.05
So to calculate crossover probability based on network size, I came up with this formula; $$\frac{e^{-\frac{1}{2}}}{\sqrt{2\pi}*{\log(\text{size})} + e^{-\frac{1}{2}}}$$
The problem is, even though DE achieved really high rewards during training, trained agents didn’t perform well during evaluation. I thought some sort of regularization of the weights might help agents to generalize better. So I applied L2 decay to mutated individuals to make them generalize better. While it helped a little bit, they were still not as good as NES (Natural Evolution Strategy) trained agents. So I combined two algorithms together, using DE to quickly explore good regions and then fine tuning the trained agents using NES. This is a good strategy because DE also performs very well in sparse reward environments such as MountainCar-v0.
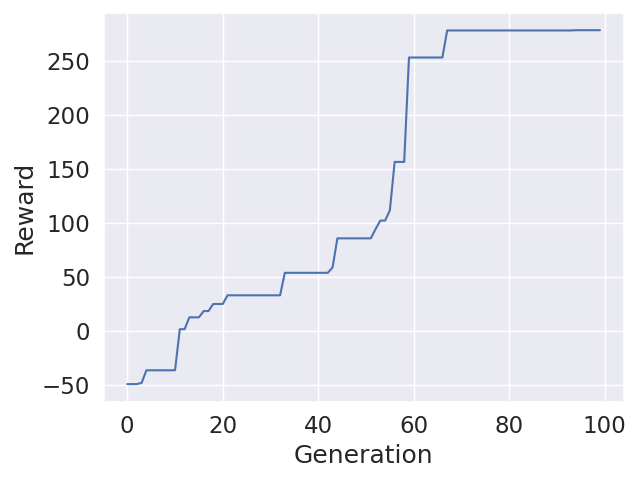
50 Generations DE and 50 Generations NES Fine Tuning
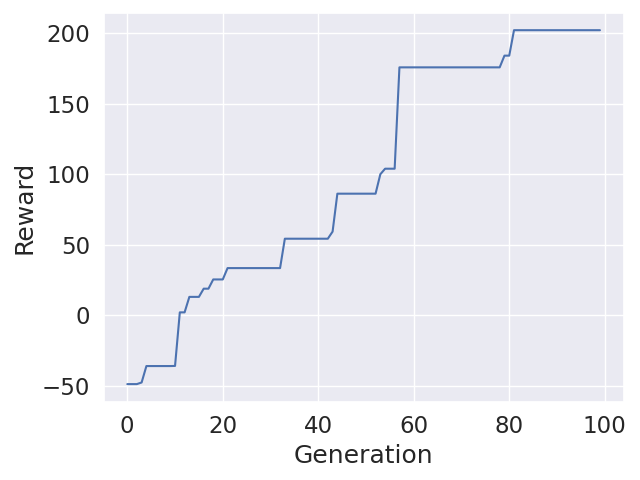
100 Generations DE
No Hidden Layer, Mutation Factor: U(0.7, 1.0), Crossover Probability: 0.0675
U(0.7, 1.0) means, in each generation the mutation factor is uniformly sampled between 0.7 and 1.0. While the both versions performed very well during training, only the fine tuned version performed reasonable during evaluation.
Fine Tuned Evaluation Reward: 260.96171919546
Only DE Evaluation Reward: 69.39153938133028
The GIF in the intro is the fine tuned policy.
In conclusion, I think differential evolution has a potentional in reinforcement learning tasks and when combined with natural evolution strategies it is a really good algorithm.
Code
https://github.com/goktug97/de-torch/blob/master/examples/finetuning.py
References
- Storn, Rainer, and Kenneth Price. “Differential Evolution – A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces.” Journal of Global Optimization, vol. 11, no. 4, Dec. 1997, pp. 341–59. Springer Link, doi:10.1023/A:1008202821328.
- Scipy.Optimize.Differential_evolution — SciPy v1.6.3 Reference Guide. https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.differential_evolution.html. Accessed 29 May 2021.
Citation
@article{karakasli2021de,
title = "Training Neural Networks with Differential Evolution for Reinforcement Learning Tasks",
author = "Karakasli, Goktug",
journal = "goktug97.github.io",
year = "2021",
url = "https://goktug97.github.io/research/training-nn-with-differential-evolution"
}