Soft Crossover for Differential Evolution

In this blog post, I experimented crossovering with polyak averaging which I named soft crossover and compared it to binomial crossover. In binomial crossover variables in the parent are replaced with the variables from the mutation vector with probabilities that are uniformly sampled between 0 and 1. In soft crossover the new candidate is calculated with the following formula; $$new\_candidate = polyak * parent + (1 - polyak) * mutation\_vector$$ where polyak is a hyperparameter between 0 and 1. I tested both crossover methods using “Test functions for optimization”. As a differential evolution strategy, I used scaledbest1bin which I introduced in A New Strategy for Differential Evolution

Experiments

For all experiments the population size is 128 and the mutation factor is 0.7.

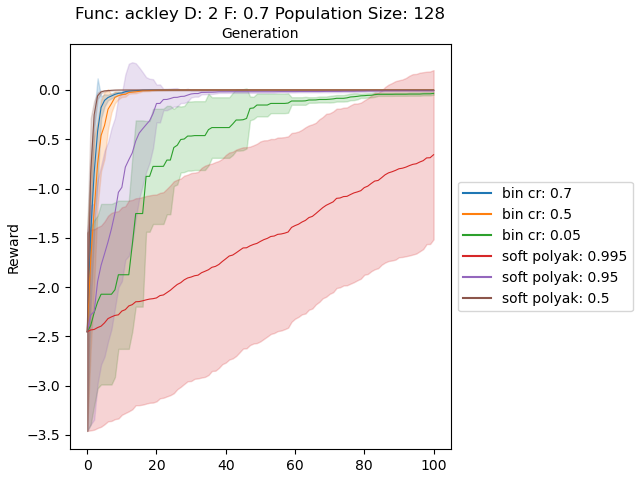
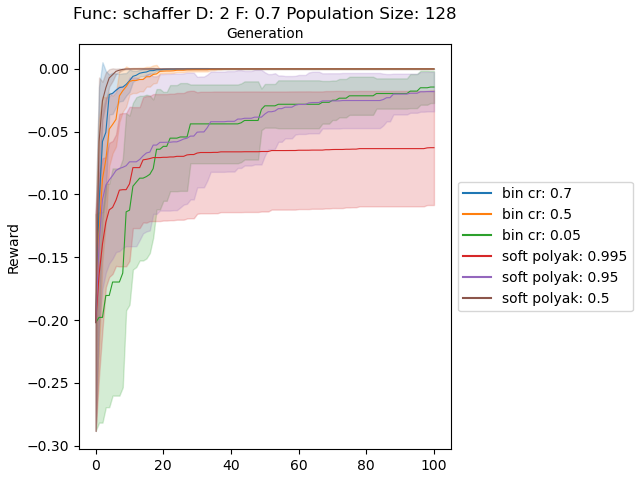
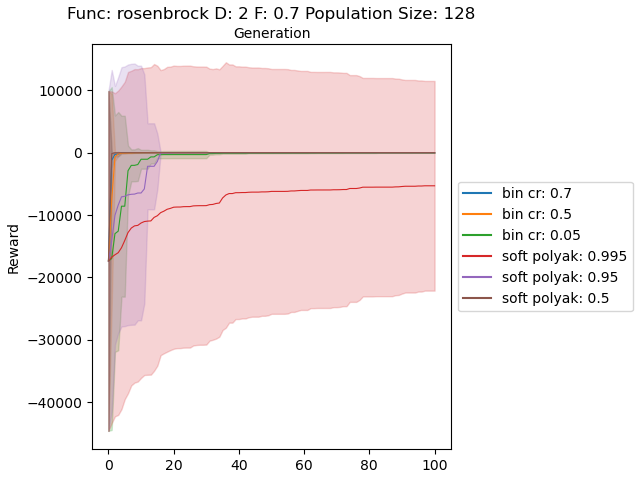
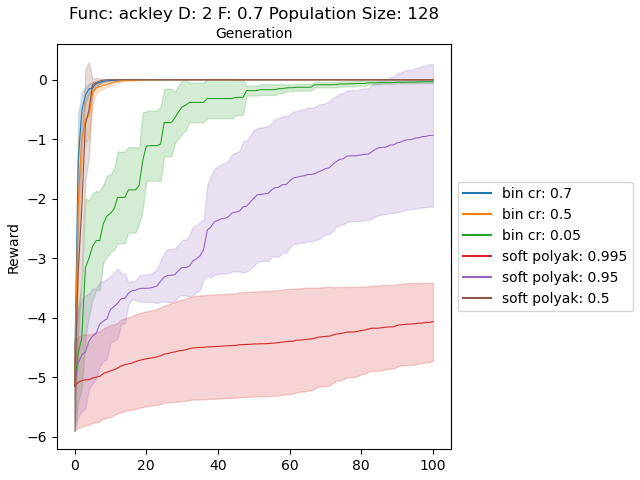
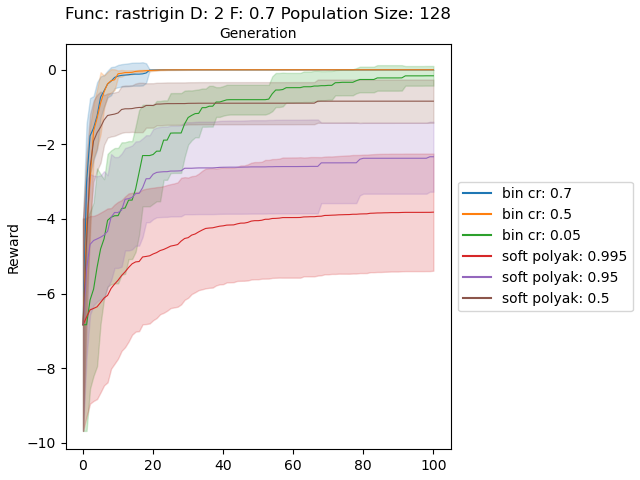
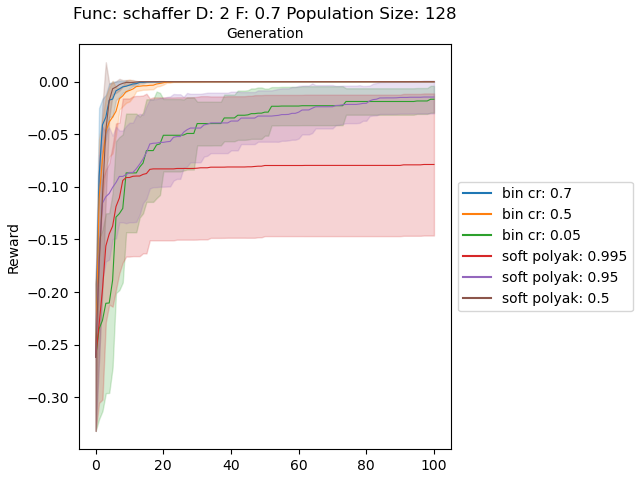
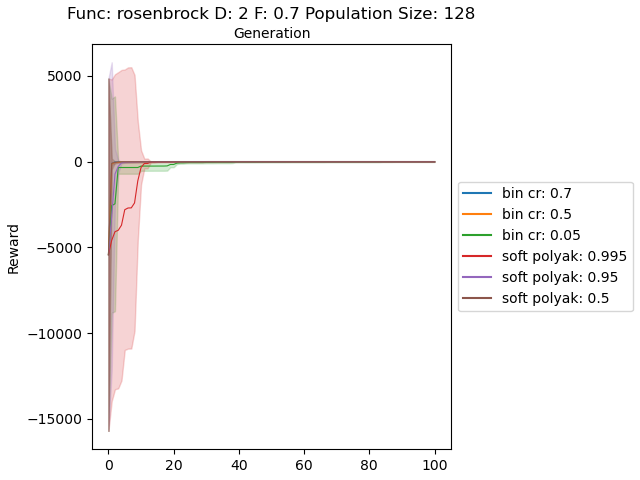
In the first experiment, I sampled the populations uniformly between the given ranges in “Test functions for optimization”. Below plots show soft and binomial crossovers performance in 2 dimensional case with different values for their hyperparemeters.

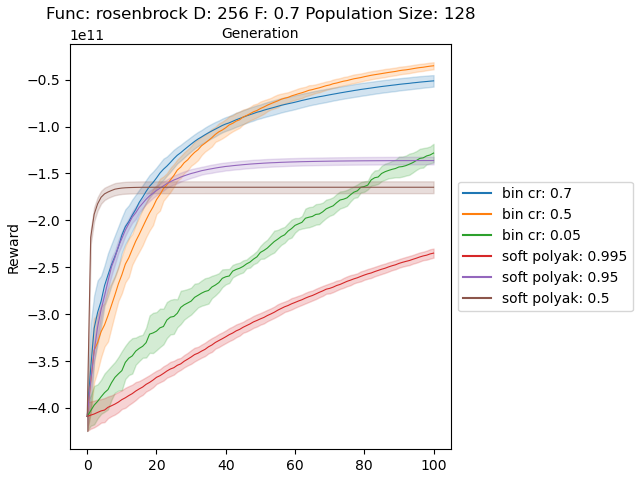
Below is 256 dimensional case for Rastrigin and Rosenbrock functions.

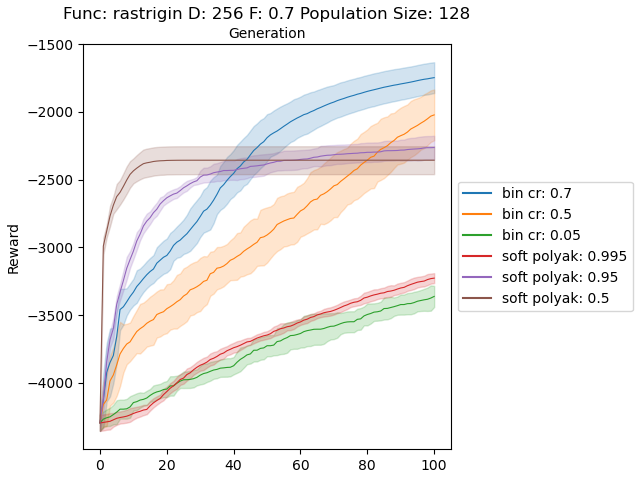
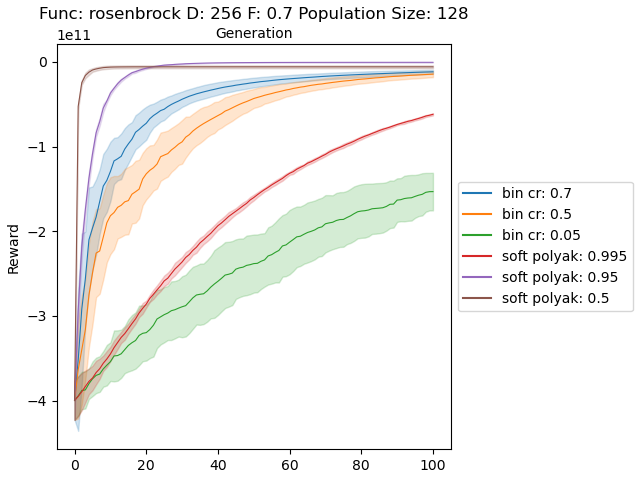
The results are very promising and soft crossover outperformed binomial crossover in every function except rastrigin. In high dimensional rastrigin function soft crossover really failed.

For the second experiment, I uniformly sampled the population between 1.0 and functions upper range. To see how robust these crossover methods are when the optimum value is outside of the initial population.

This time the best performing hyperparemeters for soft and binomial crossovers have very similar performances except rastrigin where binomial outperformed soft with a large margin.

Below plots show 256 dimensional case for this nonsymmetric initialization.

Conclusion

If the optimum point is “surrounded” by the population, soft crossover converges to global optima faster than the binomial crossover for 2D case and high dimensional case except rastrigin function. When the population is initialized such that, the optimum point is outside of the population, soft crossover is outperformed by binomial crossover. I think this method can be very reliable for neural networks because usually the “optimal solution” is inside of the population.

Code

https://github.com/goktug97/DECrossover

Also implemented in https://github.com/goktug97/de-torch

Citation

@article{karakasli2021decrossover,
  title   = "Soft Crossover for Differential Evolution",
  author  = "Karakasli, Goktug",
  journal = "goktug97.github.io",
  year    = "2021",
  url     = "https://goktug97.github.io/research/soft-crossover-for-differential-evolution"
}